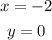Answer:
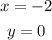
Explanation:
Given the system of equations:
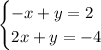
We'll multiply the first equation by 2:

Then, we'll add up both equations and solve for y, as following:
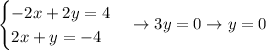
Now, we'll plug in this y-value in the second equation and solve for x, as following:
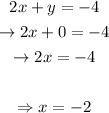
This way, we'll have that the solution to the system of linear equations is: