Answer:
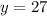
Step-by-step explanation: The statement y varies with the square of x and be translated into mathematics as follows:
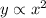
The statement implies that there is a proportional relationsip:
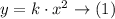
Using the condition that y = 12 when x = 2 we can calculate the value of k for the equation (1) as follows:
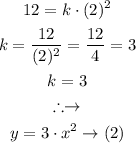
Finally, the value of y when the x = 3 is as follows:
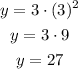
Conclusion: Therefore when x = 3 the y = 27