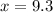
1) The best way to tackle this question is to sketch this out:
Note that, we need to know the height of that trapezoid. So, let's trace a parallel line from the vertex to the larger base of that trapezoid.
2) As we can see, we can now realize the existence of a right triangle, so let's make use of the Pythagorean Theorem to find a congruent side parallel to the height "x":
![\begin{gathered} a^2=b^2+c^2 \\ 16^2=13^2+c^2 \\ 256=169+c^2 \\ 256-169=c^2 \\ 87=c^2 \\ c=\sqrt[]{87} \\ c\approx9.3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zxrzwo6s1gis2lmls1pz313s4uso1oopuf.png)
Thus, that's the approximate measurement of x, to the nearest tenth.