Question

An unbiased 4-sided and an unbiased 6-sided dice are rolled. The score on the 6-sided dice is subtracted from the score on the 4-sided dice. Find P(positive)

Answer 1

We have two unbiased dices: one 4-sided and one 6-sided.

The event in this case is the difference between the score from the 4-sided dice and the score from the 6-sided dice.

We have to find the probability that this event is positive.

We can start by stating a result for the 4-sided dice. We start with P4 = 4, meaning that the 4-sided dice gives us a score of 4.

In order to have a positive event, the 6-sided dice has to have a score of 3 or less (NOTE: we consider the result positive if it is strictly greater than 0, meaning the a score of 4 from the 6-sided dice would result in 0 and it is not considered within the probability of the event "positive"). The event of P6 < 3 has a probability of 3/6=0.5.

Then, we can do this for the other 3 possible results of the 4-sided dice:

- If we get P4 = 3, then the 6-sided dice should have a score of 2 or less.

- If we get P4 = 2, then the 6-sided dice should have a score of 1.

- If we get P4=1, then there is no score for the 6-sided dice that makes the result positive.

Then, we can write the probabilities of each combinations of scores as:

`P=P_4(x=4)\cdot P_6(y\le3)+P(x=3)\cdot P_6(y\le2)+P(x=2)\cdot P_6(y<1)+P(x=1)\cdot P(y<0)`

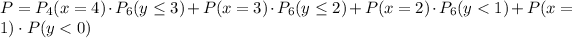
If we replace this with the probabilities, we get:

`\begin{gathered} P=P_4(x=4)\cdot P_6(y\le3)+P(x=3)\cdot P_6(y\le2)+P(x=2)\cdot P_6(y<1)+P(x=1)\cdot P(y<0) \\ P=(1)/(4)\cdot(3)/(6)+(1)/(4)\cdot(2)/(6)+(1)/(4)\cdot(1)/(6)+(1)/(4)\cdot0 \\ P=(3)/(24)+(2)/(24)+(1)/(24) \\ P=(6)/(24) \\ P=(1)/(4) \end{gathered}`

NOTE: each result from the 4-sided dice has a probability of 1/4 of happening, while each score from the 6-sided dice has a probability of 1/6.

Answer: P(positive) = 1/4 = 0.25