Jame´s age = 84
Poul´s age=8
Don's age = 28
Step-by-step explanation
Step 1
Let
x represents the age of James
y represents the age of Poul
z represents the age of Don
then
The combined ages of three relatives is 120 years.,it is
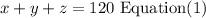
James is three times the age of Don, it is
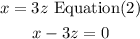
Poul is 20 years less than the age of Don,it is
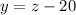
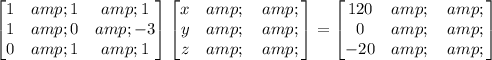
Step 2
find x, y and z
a) replace equation (2) and (3) in equation (1)
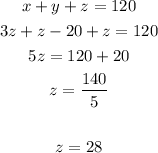
b)replace the value of z in equation (2) to find x
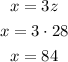
c) finally, replace the value o z in equation (3) to find y
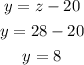
I hope this helps you