Given:
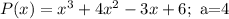
Let's use synthetic division and the remainder theorem to find P(a).
To use synthetic division, place the numbers which represents the divisor and the dividend in a long division like method.
We have:
Dividend = 1, 4, -3, 6
Divisor = 4
Now, bring down the first number (which is 1), multiply the number by the divisor, place the product under the second number, add both numbers then bring down the result.
Multiply the result by the divisor, place the result under the third number, add the numbers.
Continue with the method until you are done with the third number.
The terms under the boundary line are the results while the last number in the result is the remainder.
We have:
Therefore, the remainder is = 122
Hence, we have:
P(4) = 122
Also, using the remainder theorem, we have:
P(4).
To find P(4), substitute 4 for x in the function and evaluate:
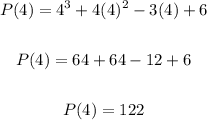
ANSWER:
P(a) = 122