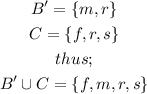Question

Sets B and C are subsets of the universal set U.These sets are defined as follows.U={f,m,q, r, s,y}B={f.q,s,y}C={f.ris)Find the following sets.Write your answer in roster form or as Ø.(a) (BAC)' = 0....O х$?(b) B'UC = 0

Answer 1

We are given the sets;

`\begin{gathered} U=\lbrace f,m,q,r,s,y\rbrace \\ B=\lbrace f,q,s,y\rbrace \\ C=\lbrace f,r,s\rbrace \\ Clearly,B,C\subseteq U \end{gathered}`

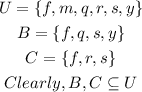
We want to find the following;

`(B\cap C)^(\prime)`

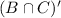
This means what is not in the intersection set but in the universal set,

The intersection set is;

`\begin{gathered} B\cap C=\lbrace f,s\rbrace \\ thus; \\ (B\cap C)^(\prime)=\lbrace m,q,r,y\rbrace \end{gathered}`
`\begin{gathered} B\cap C=\lbrace f,s\rbrace \\ thus; \\ (B\cap C)^(\prime)=\lbrace m,q,r,y\rbrace \end{gathered}`

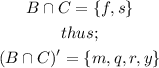
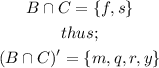
We also want to find;

`B^(\prime)\cup C`

This means the union of B complement joined with C, neglecting repititions.

We have;

`\begin{gathered} B^(\prime)=\lbrace m,r\rbrace \\ C=\lbrace f,r,s\rbrace \\ thus; \\ B^(\prime)\cup C=\lbrace f,m,r,s\rbrace \end{gathered}`