Given:
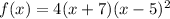
To find the real zero and its multiplicity:
Let the function equals to zero we get,
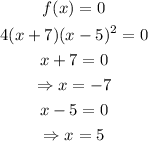
Hence, the real zeros are -7 and 5.
The zero -7, multiplicity 1, crosses the x axis.
The zero 5, multiplicity 2, touches the x axis.
Hence, the correct option is the first one.