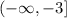Step-by-step explanation
The vertex form of a quadratic function looks like this:

Where a is the leading coefficient and (h,k) is the location of the vertex of the parabola.
The function in question 1 is a quadratic function since its greatest power of x is x². If you look at it you'll notice that its equation is written in vertex form:
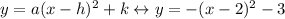
So we have a=-1, h=2 and k=-3. This implies that the vertex of this function is located at (2,-3) which is very useful if we want to sketch the graph of the function.
We'll also need to find more points that belong to the graph of the function. Remeber that this points have the form:
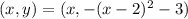
So we can take several x-values and find their respective y-values. We take x=0, 1, 3 and 4:
![\begin{gathered} x=0\rightarrow y=-(0-2)^2-3=-7 \\ x=1\rightarrow y=-(1-2)^2-3=-4 \\ x=3\rightarrow y=-(3-2)^2-3=-4 \\ x=4\operatorname{\rightarrow}y=-(4-2)^2-3=-7 \end{gathered}]()
So now we know that the vertex of the parabola is (2,-3) and that it also passes through the points (0,-7), (1,-4), (3,-4) and (4,-7).
Regarding the domain of the function, the domain of any quadratic function is always composed of all the real numbers.
On the other hand, the range of a quadratic function depends on the y-value of its vertex. This value is always the minimum or the maximum value of y depending on the sign of a. If the leading coefficient a is negative then the y-value of the vertex is the maximum y-value of the graph. If a is positive then the y-value of the vertex is the minimum y-value. In this case a=-1 which is negative. Then the y-value of the vertex -3 is the maximum y-value and the range of the function is composed of all the numbers equal or smaller than -3.
Answer
Then the graph is:
The domain of the function is:
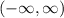
And the range of the function is: