Question

Question 1: Radiation emitted from human skin reaches its peak at A = 940 uma. What is the frequency of this radiation?b. What type of electromagnetic waves are these?C. How much energy (in electron volts) is carried by one quantum ofthis radiation?

Answer 1

Given:

λ = 940 μm

Let's solve for the following:

• (a). What is the frequency of this radiation?

To find the frequency, apply the formula:

`f=(c)/(\lambda)`

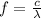
Where:

f is the frequency

c is the speed of light = 3 x 10⁸ m/s

λ = 940 μm

Thus, we have:

`\begin{gathered} f=(3*10^8)/(940*10^(-6)) \\ \\ f=3.19*10^{11\text{ }}Hz. \end{gathered}`

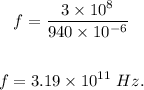
Therefore, the frequency of this radiation is 3.19 x 10¹¹ Hz.

• (b). What type of electromagnetic waves are these?

Since the wave has a frequency of 3.19 x 10¹¹ Hz, the wave will be said to be an infrared.

• (c). How much energy (in electron volts) is carried by one quantum of this radiation?

Apply the formula:

`E=h*f`

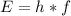
Where:

E is the energy in Joules

h is Planck's constant = 6.626 x 10⁻³⁴

f is the frequency gotten in part A.

We have:

`\begin{gathered} E=6.626*10^(-34)*3.19*10^(11) \\ \\ E=2.11*10^(-22)\text{ J} \end{gathered}`

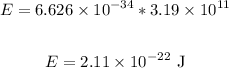
Now, to convert from Joules (J) to electron volts (eV), we have:

`\begin{gathered} 2.11*10^(-22)*(\frac{1\text{ eV}}{1.602*10^(-19)}) \\ \\ =1.32*10^(-3)\text{ eV} \end{gathered}`

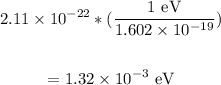
Therefore, the energy in electron volts is 1.32 x 10⁻³ eV.

ANSWER:

• (a). 3.19 x 10¹¹ Hz.

• (b). Infrared

• (c). 1.32 x 10⁻³ eV.