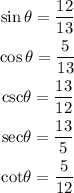Answer:
The exact values of the remaining trigonometric functions of (theta) satisfying the given conditions are;
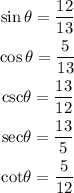
Step-by-step explanation:
Given the above conditions;
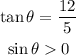
The only quadrant where the value of tangent and sine is positive is the first quadrant.
So, the value of cosine will also be positive since in the first quadrant sine, cosine and tangent are positive (greater than zero).
Given;

We need to calculate the hypotenus using pythagoras theorem;
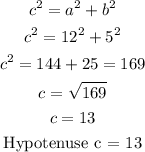
we can use this values to find the exact values of the following;
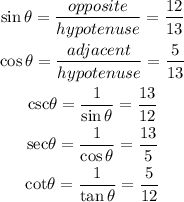
Therefore, the exact values of the remaining trigonometric functions of (theta) satisfying the given conditions are;