Question

You throw a ball straight up with an initial velocity of 16 m/s on the way up it passes a tree branch 7.4 m above the release height. How much additional time will pass before the ball passes the tree branch on the way back down?

Answer 1

Given:

Initial velocity = 16 m/s

It passes a tree branch 7.4 meters above the release height.

Let's find the additional time that will pass before the bass passes the tree on the way back down.

Apply the kinematics formula:

`y=v_it+(1)/(2)at^2`

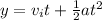
Where:

y is the height

t is the time

a is acceleration due to gravity.

vi is the initial velocity

Rewrite the equation for t:

`t=(-v_1\pm√(v_i^2+2ay))/(a)`

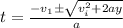
Plug in the values and solve for the time, t.

We have:

`\begin{gathered} t=(-16\pm√(16^2+2(-9.8)(7.4)))/(-9.8) \\ \\ t=(-16\pm√(256-145.04))/(-9.8) \end{gathered}`

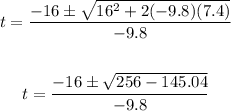
Solving further:

`\begin{gathered} t=(-16\pm√(110.96))/(-9.8) \\ \\ t=(-16\pm10.534)/(-9.8) \\ \\ t_1=(-16-10.534)/(-9.8)\text{ and }t_2=](-16+10.534)/(-9.8) \\ \\ t_1=2.71\text{ and t2 = 0.56} \end{gathered}`

The time that will pass is the difference between t1 and t2:

t1 - t2 = 2.71 - 0.56 = 2.15 seconds

Therefore, the additional time that will pass before the ball passes the tree branch on the way back down is 2.15 seconds.

ANSWER:

2.15 seconds