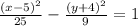We are given the following information
Foci at (0, -4) and (10, -4)
The conjugate axis is 6 units
Recall that the standard form of the equation of hyperbola centered at (h, k) is given by
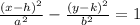
Where the center is (h, k)
The center (h, k) is the midpoint of the transverse axis given by
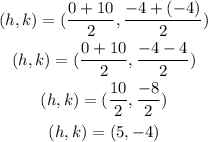
Let us find the values of a and b
The semi transverse axis (a) is given by
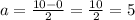
The semi conjugate axis (b) is given by
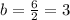
So, the equation of the hyperbola is
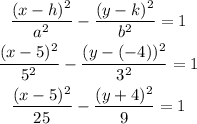
Therefore, the equation of the hyperbola is