ANSWER
Step-by-step explanation
Of the boxes that say the length and width of the prism, we have to see which ones have 24 as a product - since this is the area of the base. There are two - the two on the left - the first one:
![A=l* w=6\operatorname{cm}*4\operatorname{cm}=24\operatorname{cm}^2]()
This is correct, because the area is 24cm²
The second one:

This is not the right base area, so these dimensions are not right.
Then, with the rest of the dimensions we have the height. The volume of a prism is the product of its dimensions or, in other words, the product of the area of the base and its height. Therefore, since we know that the area of the base is 24, we just have to multiply that by the given height and see which ones give not a whole number as a result.
24 is a whole number, so when it is multiplied by a whole number the result is another whole number, so the options where the height is a whole number can't be right.
Then we just have to see if the mentioned product with the heights of the remaining options is a decimal.
For the bottom option in the middle: height = 15.1:

Not a whole number --> correct
For the upper option on the right: height 8.4:
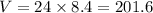
Not a whole number --> correct