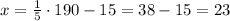ANSWERS
13. $195 (24 months) and $130 (11 months)
14. $80 (1 month) and $100 (5 months)
15. 10 months ($125) and 23 months ($190)
16. 5
18. 75
19. y = 5x + 75
Step-by-step explanation
To answer all of these questions we have to find the equation first.
The equation that relates the account balance (y) to the number of months saving (x) is,

Where m is the slope - also called rate of change, and b is the y-intercept.
The slope of a line passing through points (x1, y1) and (x2, y2) is,
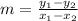
We can find the slope by choosing any two pairs of (# of months, account balance). Let's find it with the pairs (2, 85) and (6, 105),
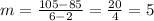
The slope of the line is 5, so for now, the equation is,
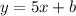
To find the y-intercept we have to replace y and x with any pair of points from the table and solve for b. Let's use the first one,
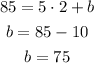
The y-intercept is 75. And the equation is y = 5x + 75.
To find the answers to the questions in parts 13 and 14, we just have to replace x by the number of months given and solve:
• 24 months,
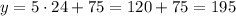
• 11 months,
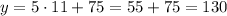
• 1 month,
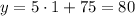
• 5 months,
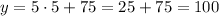
To solve the two questions in part 15 first we have to solve the equation for x. Subtract 75 from both sides,
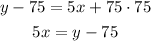
And divide both sides by 5,
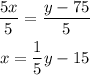
So if we want to find the number of months until she saved $125, we have to replace y with 125,
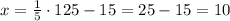
And the same applies to $190,