Question

a basketball player's "hang time" is the amount of time the player remains suspended in the air after a jump.the height (in meters) of superstar michael jordan during a jump is shown in the graph below. assume that h is the distance from the ground to the lowest part of his body at t seconds.complete the following sentences based on the graph of the function.round your answers to the nearest tenth.* This is the graph of a (nonlinear, linear or constant) function.* Michael Jordan's hang time is ___ second(s).* The maximum height is about ___ meter(s).* For t between t - 0.5 and t - 1. the height is (increasing, decreasing or constant).

Answer 1

* This is the graph of a (nonlinear, linear or constant) function.

Answer:

This is the graph of a nonlinear equation. In this case is the graph of a quadratic equation of the form:

`\begin{gathered} y(x)=ax^2+bx+c \\ where \\ a\in R,b\in R,c\in R \end{gathered}`

-------------------------------------------------------------------

Michael Jordan's hang time is ___ second(s).

Answer:

From the graph, we can see that the domain of the function is approximately:

`D\colon0\le t\le0.9`

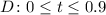
So, we can conclude that Michael Jordan's hang time is 0.9 seconds

-------------------------------------------------

* The maximum height is about ___ meter(s).

Answer:

From the graph, we can see that the vertex of the function is located approximately at:

`y=(0.5+0.4)/(2)=0.45`

So, we can conclude, that The maximum height is about 0.45 meters

---------------------------------------------

* For t between t - 0.5 and t - 1. the height is (increasing, decreasing or constant).

Answer:

From the graph we can see that:

`\begin{gathered} From\colon \\ t=0.5 \\ to \\ t=1 \end{gathered}`

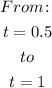
The height is decreasing.