Question

suppose that the initial amount of an element is 120 grams. The amount remaining after t days can be modeled by the equation y=120x0.93^t. Use a graph to determine the half life.

Answer 1

Given the equation:

`y=120\cdot0.93^t`

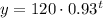
we know that the half life is the amount of time it takes for there to be half the initial amount. Therefore, since the initial amount is 120, then for the half life will be y=60, then:

`\begin{gathered} 60=120\cdot0.93^t \\ \Rightarrow(60)/(120)=0.93^t \\ \Rightarrow(1)/(2)=0.93^t \end{gathered}`

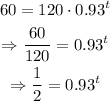
Now we apply natural logarithm on both sides of the equation to solve for t:

`\begin{gathered} \ln ((1)/(2))=\ln (0.93^t) \\ \Rightarrow\ln ((1)/(2))=t\cdot\ln (0.93) \\ \Rightarrow t=(\ln (0.5))/(\ln (0.93))=9.55 \\ t=9.55 \end{gathered}`

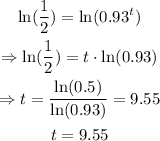
therefore, we have that the half life will be after 9.55 days, and we can watch this on the graph of y: