Given:
Angle between distance kasey's feet and the top of the lampost is 62°.
The distance between their bases is 13 feet.
The objective is to find the height of the malpost.
The given situation can be represented as,
Here, AB represent lampost and point C represents position of kasey.
In the right angled triangle, AC is hypotenuse side, BC is adjacent side and AB is opposite side.
The height of the lampost can be calculated using trigonometric ratio of tanθ.
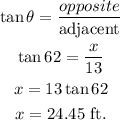
Hence, the height of the lampost is 24.45 ft.