Step-by-step explanation:
Let the following function:
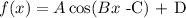
by definition, the amplitude of this function is the absolute value of A.
Now, consider the following function:
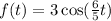
then, by definition, the amplitude of this function would be:
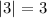
now, to find the minimum output of the given function we can use the first derivative criterion:
Notice that the critical points would be:

now, the domain of f(x) is:
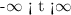
thus, the interval where the function is decreasing is:
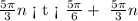
and the interval where the function is increasing is:
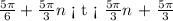
thus, we can conclude that the minimum output occurs when
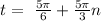
and this output would be - 3.
Then, the correct answer is:
Answer: