Question

The radioactive substance uranium240 has a halflife of 14 hoursThe amount of a sample of uranium-240 remaining (in grams) after hours is given by the following exponential function A(i) = 3900 * (1/2) ^ (1/14)

Answer 1

GIVEN:

We are given the function that models the decay of the substance uranium-240.

`A(t)=3900((1)/(2))^{(t)/(14)}`

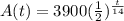
Required;

Find the initial amount in the sample

Find the amount remaining after 50 hours.

Step-by-step solution;

What we have here is an exponential function with the variable t denoting the number of hours and A(t) denotes the population after t hours.

To determine the initial amount in the sample, we take t = 0 and solve as follows;

`\begin{gathered} A(0)=3900((1)/(2))^{(0)/(14)} \\ \\ A(0)=3900((1)/(2))^0 \\ \\ A(0)=3900*1 \\ \\ A(0)=3900 \end{gathered}`

To find the amount remaining after 50 hours;

`\begin{gathered} A(50)=3900((1)/(2))^{(50)/(14)} \\ \\ A(05)=3900((1)/(2))^(3.57142857143) \\ A(50)=3900*0.0841187620394 \\ \\ A(50)=328.063171954 \\ \end{gathered}`

Rounded to the nearest gram we now have;

`A(50)=328gms`

Therefore,

ANSWER:

Initial amount in the sample = 3900 grams

Amount after 50 hours = 328 grams