Question

Rewrite the equation of a circle given below in standard form x² + 6x + y² - 16y = 23

Answer 1

`x^2+6x+y^2-16y=23​`

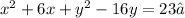
The standard form of the equation of a circle is:

`(x-h)^2+(y-k)^2=r^2`
`\begin{gathered} x^2+6x+y^2-16y=23​ \\ (x^2+6x+a)+(y^2-16y+b)=(23​+a+b) \end{gathered}`

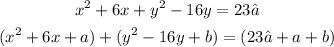
To answer this we have to think of the numbers a and b to form a a trinomial (for x and y) that is reducible to the form (x-h)^2 and (y-k)^2 respectively. We call this completing the square. If you recall the special products below, here we will be doing that but in reverse.

`(x\pm y)^2=x^2\pm2xy+y^2`

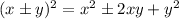
The value of a is always the square of the half of the coefficient of x ( which in this case is 6). Thus, a = 9. While b is always the square of the half of the coefficient of y ( which in this case is -16). Thus, b = 64. If we substitute the value of a and b , the resulting equation is:

`(x^2+6x+9)+(y^2-16y+64)=(23​+9+64)`

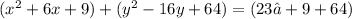
At this point , you can factor each of the trinomials (of x and y) into a form similar to (x-h)^2 and (y-k)^2 respectively.

`\begin{gathered} (x^2+6x+9)+(y^2-16y+64)=(23​+9+64) \\ (x+3)^2+(y-8)^2=96 \end{gathered}`

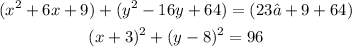
The standard form of the equation the circle is :

`(x+3)^2+(y-8)^2=96`

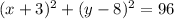
it gives us the following information about the coordinates of its center and the radius of the circle.

In this equation the center is at (-3,8) and the radius is sq.root of 96.