Question

Graph A Graph B 5 2 X X 3 2 3 4 5 Which table and graph represent the equation y = 2x? O A. Table B and graph A O B. Table A and graph B O C. Table B and graph B O D. Table A and graph A

Answer 1

Given:

The equation is y = 2x.

The objective is to find which of the table values match the with a given graphs.

The general equation of straight line is,

`y=mx+c`

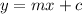
Here, m represents the slope and b represents the y intercept.

Consider the graph A and find the slope of the equation.

Take two coordinates from the graph as,

`\begin{gathered} (x_1,y_1)=(0,0) \\ (x_2,y_2)=(1,2) \end{gathered}`

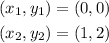
The formula to find the slope of the equation is,

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(2-0)/(1-0) \\ m=(2)/(1) \\ m=2 \end{gathered}`

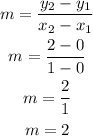
Fro mthe graph A, the value of y intercept is 0.

Substitute the obtained values in the equation of straight line.

`\begin{gathered} y=2x+0 \\ y=2x \end{gathered}`

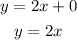
Thus, the given equation, coordinates of the table A matches with the graph A.

Hence, option (D) is the correct ant