Question

I have an exercise that I am confused about this exercise is helping me prepare for a GED test I have not looked at Math since my children were in high school I'm 61 years old I really could use some help and guidance in this exercise I really need help construction is distribution table I have no idea where we can with any of this●Suppose we know that the birth weight of babies is normally distributed with mean 3500g and standard deviation 500g. ● What is the probability that a baby is born with weight less than 3100g? Hint find the z-score, and construct the standard normal distribution density curve, then shade your seeking area and find the probability from the table.● If 25 newborn babies are randomly selected, what is the probability that the 25 babies are born that their mean weigh less than 3100g? ●Hint find the z-score, construct the standard normal distribution density curve, shade your seeking area then find the probability

Answer 1

Population:

Mean (μ): 3500 g

Standard deviation (σ): 500g

(a)

The z-score for this distribution can be calculated using the formula:

`Z=(X-\mu)/(\sigma)...(1)`

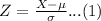
The z-score of X = 3100 g is:

`Z=(3100-3500)/(500)=(400)/(500)=-0.8`

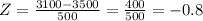
Now, to find the probability that a baby is born with a weight less than 3100 g, we calculate the probability of Z < -0.8 in a standardized distribution:

`P(X\lt3100\text{ g})=P(Z\lt-0.8)=0.2118554`

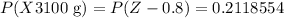
As we can see, the probability is approximately 0.212, and the corresponding shaded area is:

(b)

Sample size = 25

The z-score for the distribution of the sample mean can be calculated using the formula:

`Z=\frac{\bar{X}-\mu}{\sigma/√(n)}`

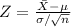
Where n is the sample size. Now, we calculate the z-score for a mean of 3100 g:

`Z=(3100-3500)/(500/√(25))=(-400)/(500/5)=-4`

Finally, the probability that the 25 babies are born with a mean weight less than 3100 g is:

`P(Z\lt-4)=0.0000317`

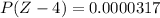
As we can see, the probability is approximately 0.0000317, and the corresponding shaded area is: