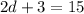We can translate algebraically this problem as follows:
1. Let d the number of doughnuts.
2. When we say that Jim "had three more" we are adding here.
3. When we say "twice the number of doughnuts as Jane" we are multiplying here.
Then, we can translate the situation - algebraically - as follows:
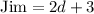
If Jim had 15 doughnuts, then the equation to find out the number of doughnuts Jane had is:
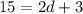
Which is equal to: