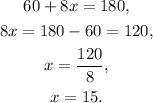Answer:
To answer this question we will use the following diagram as reference:
Recall that the interior angles of an equilateral triangle measure 60 degrees each.
Now, notice that angles A and B form a linear pair, meaning that:
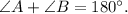
Substituting ∠A=60°, ∠B=8x° in the above equation we get:
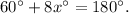
Solving the above equation for x, we get: