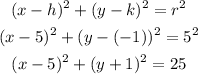Question

What is the equation of the circle that has a diameter with endpoints (2,-5) and (8,3)?

Answer 1

The equation of the circle has the following form:

`(x-h)^2+(y-k)^2=r^2`

Where

(h,k) are the coordinates of the center of the circle

r represents the radius of the circle

First, let's determine the radius of the circle:

We know that the circle has a diameter with endpoints (2,-5) and (8,3). To determine the length of the diameter you have to calculate the distance between both points, using the following formula:

`d=\sqrt[]{(x_1-x_2)^2+(y_1-y_2)^2}`

Where

(x₁,y₁) are the coordinates of one of the endpoints of the diameter

(x₂,y₂) are the coordinates of the second endpoint of the diameter

Replace (8,3) as (x₁,y₁) and (2,-5) as (x₂,y₂) on the formula to determine the diameter:

`\begin{gathered} d=\sqrt[]{(8-2)^2+(3-(-5))^2} \\ d=\sqrt[]{(8-2)^2+(3+5)^2^{}} \\ d=\sqrt[]{6^2+8^2} \\ d=\sqrt[]{36+64} \\ d=\sqrt[]{100} \\ d=10 \end{gathered}`

The diameter of the circle is d=10 units, divide it by 2 and you get that the radius of the circle is r= 5 units

Center of the circle

The center of the circle is the midpoint of the diameter, to determine its coordinates you have to work with the x and y coordinates of the endpoints. I will call the center of the circle as point "C"

x-coordinate of the center

The x-coordinate of the midpoint is halfways the distance between the x-coordinates of the endpoints. So you have to calculate the difference between the x-coordinates of the endpoints and divide it by 2:

x₁= 8

x₂= 2

`\begin{gathered} \text{d}_(xC)=(x_1-x_2)/(2)_{} \\ d_(xC)=(8-2)/(2) \\ d_(xC)=(6)/(2) \\ d_(xC)=3 \end{gathered}`

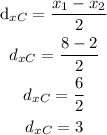
The distance over the x-axis, between the endpoints and the midpoint, is 3 units.

To calculate the x-coordinate of C, add this distance to the x-coordinate of the endpoint (2,-5)

`\begin{gathered} x_C=x_2+d_(xC) \\ x_C=2+3 \\ x_C=5 \end{gathered}`

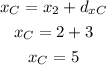
y-coordinate of the center

To determine this coordinate you have to work with the y-coordinates of the endpoints.

As before, the first step is to determine the distance over the y-axis between both endpoints and the midpoint.

y₁=3

y₂=-5

`\begin{gathered} d_(yC)=(y_1-y_2)/(2) \\ d_(yC)=(3-(-5))/(2) \\ d_(yC)=(3+5)/(2) \\ d_(yC)=(8)/(2) \\ d_(yC)=4 \end{gathered}`

The distance between the endpoints and the midpoint over the y-axis is 4 units

To calculate the y-coordinate of the center, you can subtract the calculated distance to the y-coordinate of the endpoint (8,3)

`\begin{gathered} y_C=y_1-d_(yC) \\ y_C=3-4 \\ y_C=-1 \end{gathered}`

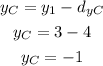
So the coordinates of the center of the circle are: C(5,-1)

Now we can determine the equation of the circle, replace the formula with h=5, k=-1, and r=5

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ (x-5)^2+(y-(-1))^2=5^2 \\ (x-5)^2+(y+1)^2=25 \end{gathered}`