Question

Julia invested $17,000 in an account paying an interest rate of 2.4% compounded daily. Assuming no deposits or withdrawals are made, how long would it take, to the nearest tenth of a year, for the value of the account to reach $21,400?

Answer 1

To solve this problem, we must use the formula for Compound Interest:

`P_N=P_0\cdot(1+(r)/(k))^(N\cdot k).`

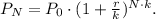
Where:

• P_N is the balance in the account after N years,

,

• P_0 is the starting balance of the account (also called an initial deposit, or principal),

,

• r is the annual interest rate in decimal form,

,

• k is the number of compounding periods in one year.

In this problem, we have:

• P_0 = $17,000,

,

• P_N = $21,400,

,

• r = 2.4% = 0.024,

,

• k = 365 (the interest rate is compounded daily).

Replacing the data of the problem in the equation above, we have:

`21400=17000\cdot(1+(0.024)/(365))^(N\cdot365)\text{.}`

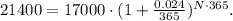
Solving for N the last equation, we get:

`\begin{gathered} (21400)/(17000)=(1+(0.024)/(365))^(N\cdot365), \\ \ln ((21400)/(17000))=N\cdot365\cdot\ln (1+(0.024)/(365)), \\ N=(\ln((21400)/(17000)))/(365\cdot\ln(1+(0.024)/(365)))\cong9.6. \end{gathered}`

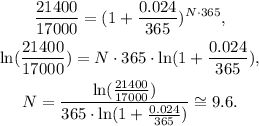
Answer

To the nearest tenth of a year, it will take 9.6 years for the account to reach $21,400.