Question

I asked someone to help me earlier but class cut out before they could answer my question

Answer 1

Given that the boat travels upstream for 60 miles in 4 and downstream for 60 miles in 3 hours.

Let x be the rate of the boat in still water.

Let y be the rate of the boat in the current.

Downstream =x+y.

Upstream =x-y.

Using the speed formula for downstream, we get

`3(x+y)=60`

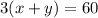
Dividing both sides by 3, we get

`(3\mleft(x+y\mright))/(3)=(60)/(3)`
`x+y=20`
`x=20-y`

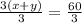
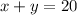
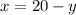
Using the speed formula for upstream, we get

`4(x-y)=60`

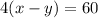
Dividing both sides by 4, we get

`(4\mleft(x-y\mright))/(4)=(60)/(4)`

`x-y=15`

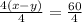
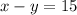
Substitute x=20-y to compute y value, we get

`20-y-y=15`

`-2y=15-20`

`-y=(-5)/(2)=-2.5`
`y=2.5`

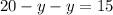
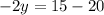
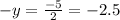
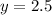
Substitute y=2.5 in x=20-y, we get

`x=20-2.5=17.5`

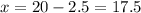
Hence the rate of the boat in still water is 17.5 mph and the rate of the boat in the current is 2.5 mph.