Question

Find the balance in the account after the given period.$7000 principal earning 7% compound annually, 7 yearsThe balance after 7 years will be $___(I'm sorry if it's confusing, I worded the question word for word)

Answer 1

The balance after 7 years will be $11240.60

Step-by-step explanation:

We would apply the compound interest formula:

`FV\text{ = P(1 + }(r)/(n))^(nt)`

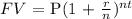
FV = future value = balance,

P = Principal = $7000

r = interest rate = 7%

n = number of times compounded per year = annually = 1 year

t = time = 7 years

`FV\text{ = 7000(1 + }(0.07)/(1))^(1*7)`
`\begin{gathered} FV=7000(1+0.07)^7\text{ } \\ =7000(1.07)^7\text{ = 7000(}1.6058) \\ FV=\text{ \$11240.6} \end{gathered}`

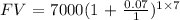
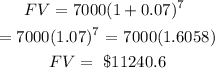
The balance after 7 years will be $11240.60