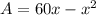
Step-by-step explanation
here we have a rectangle, the perimeter of a recntangle is given by
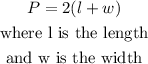
Step 1
Let
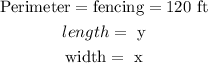
replace
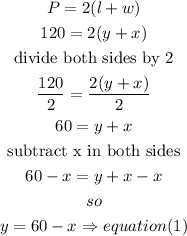
so, the equation that relates x and y is
y=60-x
Step 2
now, lets find an expression for the area
the area of a rectangle is given by
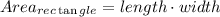
therefore, the area would be
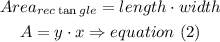
now, replace the y value from equation(1) into equation(2)
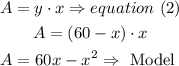
therefore, the model of equation that shows the relation between the area and the width(x) is
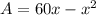
Step 3
graph:
a) make a table
i) when x= 0
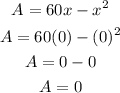
therefore, when the width (x) is 0 the area(A) is zero, obvious but a good example
so, a point of the graph is
(0,0)
ii) when x =1
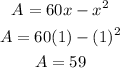
so, the point is (1,59) , when the width is 1, the area is 59
iii) when x = 3
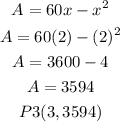
draw a line that passes trought the points
there is a restriction
the area can not be negative, so it must be greater than 0
so

therefore, the width(x) must be equal or smaller than 60
I hope this helps you