Question

Craig shoots a basketball at an angle of 55" from the horizontal. It leaves his hands 6 feet from the ground with a velocity of 21 ft/s.Step 2 of 2: Determine the height of the ball when it is 2 feet away horizontally. Round to the nearest tenth.AnswerHow to enter your answer (opens in new window)okay

Answer 1

8.422 ft

Step 1

given:

`\begin{gathered} x=12t \\ y=-16t^2+17.2t+6 \end{gathered}`

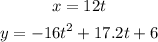
hence

a)find the time wich the distance horizontally is 2 ft

so

let

`x=2`

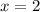
now ,replace and solve for t

`\begin{gathered} x=12t \\ 2=12t \\ divide\text{ both sides by 12} \\ (2)/(12)=(12t)/(12) \\ (1)/(6)=t \\ t=(1)/(6)\text{ seconds} \end{gathered}`

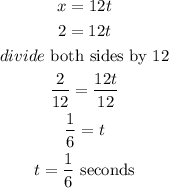
b)now, find the heigth for the given time

let

`t=\text{ }(1)/(6)\text{ sec}`

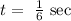
now, replace in the parametric equation

`\begin{gathered} y=-16t^2+17.2t+6 \\ y=-16((1)/(6))^2+17.2((1)/(6))+6 \\ y=-(16)/(36)+(17.2)/(6)+6 \\ y=-0.4444+2.8666+6 \\ y=8.422 \end{gathered}`

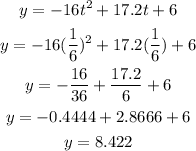
therefore, the answer is

8.422 ft

I hope this helps you