Answer:
• (7x-1)(x-3)=0
,
• x=1/7 or 3
Step-by-step explanation:
Given the quadratic equation:
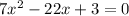
First, multiply the first and the last term:
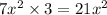
Next, find factors of the product above that add up to the middle term:
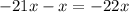
Therefore, we obtain the factored form below:
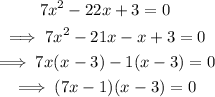
The equation in factored form is:
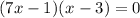
Next, solve for x:
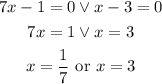
The solution to the equation is x=1/7 or 3.