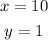1 Answer

Tterrace · Answer 1 · 2023-10-03T14:01:52+0000

Given the following System of equations:

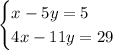
$\begin{cases}x-5y=5 \\ 4x-11y=29\end{cases}$

You can solve it using the Elimination method. Follow the steps shown below:

1. Multiply the first eqeuation by -4,

2. Add the equations.

3. Solve for the variable "y".

Then:

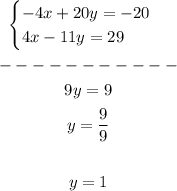
$\begin{gathered} \begin{cases}-4x+20y=-20 \\ 4x-11y=29\end{cases} \\ ----------- \\ 9y=9 \\ y=(9)/(9) \\ \\ y=1 \end{gathered}$

4. Now you must substitute the value of the variable "y" into any original equation.

5. Solve for the variable "x".

Then, you get:

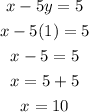
$\begin{gathered} x-5y=5 \\ x-5(1)=5 \\ x-5=5 \\ x=5+5 \\ x=10 \end{gathered}$

The solution is:

$\begin{gathered} x=10 \\ y=1 \end{gathered}$

Please log in or register to add a comment.