SOLUTION
Given the question in the question tab, the following are the solution steps to get possible 5 card hands
Step 1: Identify the type of problem in the question
Ian is choosing a subset of size 5 from a set of size 52. Note that the order in which he is dealt these 5 cards is irrelevant. Thus, order doesn’t matter. Thus, this is a combination problem.
Step 2: Write the formula for finding combination
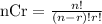
Step 3: Find the possible different 5 card hands
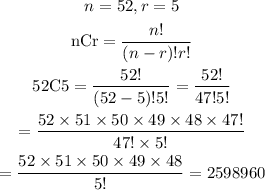
Hence, there are 2598960 different possible card hands.