Let:
x = Investment in the first year
y = Investment in the second year
Since connor had 91.00 to invest:
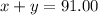
Using the simple interest formula:
For 16%:
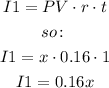
For 14%:
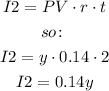
After one year, the total interest earned was $13.74. so:
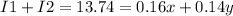
So:
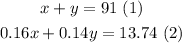
From (1):
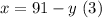
Replace (3) into (2):
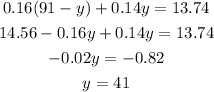
Replace the value of y into (3):
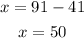
He invested $50 at 16% and $41 at 14%