Question

Adal, or quadratic functionI got it!I'm still learning itYou have to decide which of two prizes you will accept!Prize A: 55,000 for the first month with a $100 increase every month thereafter.Prize : 52.000 for the first month with a 10% increase every month thereafter.9. Create an equation for each situation (Prize A and Prize 3) (2 points)MonthPrize AMonthlyAmountY:Prize BMonthlyAmounta is Pin =5000+1000(n-1)bis Pin=20000/911-0.1012s10. Use each equation to complete the table to the right (2points)-When will prizes earn more than prize (point)5I622. How much more will prizes earn than prize in the month( pot)20::

Answer 1

In question 9, we want an equation for each situation, that is, how much is the monthly amount of each prize.

Let'use the variables in the table,, x for month, y₁ for monthly amount of A and y₂ monthly amount for B.

Assuming x = 0 is the first month, in A we will have 5000 plus 100 increase for each month thereafter.

Inthe first month, x = 0, there is no increase, and x = 1 has one increase, and so on.

So, the amount it had increases so far is x times 100. Plus the starting 5000, we will have the equation:

`y_1=5000+100x`

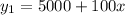
For prize B, we start with 2000 and have a 10% increase. 10% increase is the same as multiplying by 100% + 10% each month, that is, multiply by 1.10.

This multiplication accumulates over the months, so we have to exponentiate it by the number of months. The equation becomes:

`y_2=2000\cdot(1.10)^x^{}`

We can see that in the first month, x = 0, so we will have the initial 2000 correctly.

Now, we can complete the table by substituting x into the equations:

x = 0:

`\begin{gathered} y_1=5000+100\cdot0=5000 \\ y_2=2000\cdot(1.10)^0=2000 \end{gathered}`

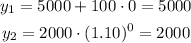
x = 1:

`\begin{gathered} y_1=5000+100\cdot1=5100 \\ y_2=2000\cdot(1.10)^1=2200 \end{gathered}`

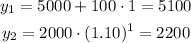
x = 2:

`\begin{gathered} y_1=5000+100\cdot2=5200 \\ y_2=2000\cdot(1.10)^2=2420 \end{gathered}`

And so one until x = 12.

We will get the table: