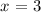Question: Solve the equation:
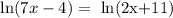
Solution:
applying the laws of logarithms (applying the inverse function of the logarithm function) we get:
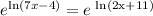
this is equivalent to:

putting similar terms together we get:
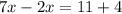
this is equivalent to:
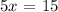
solving for x, we get:
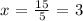
then, we can conclude that the solution of the equation is: