Let's use the variable x to represent the number of jeans and y to represent the number of t-shirts.
The price paid for x jeans is 20x and the price paid for y t-shirts is 10y.
If the total cost is $350, we can write this equation:
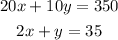
The number of items is 25, so we can write a second equation:
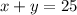
Subtracting the first and second equations, we have:
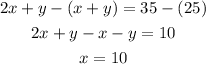
Now, solving the second equation for y:
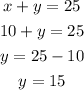
Therefore she bought 10 pairs of jeans and 15 t-shirts.