Given the functions:
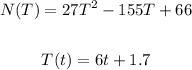
Where:
T is the temperature of the food.
t is the time in hours.
Let's solve for the following:
• (a). Find the composite N(T(t).
To find the composite function, we have:
N(T(t)) = N(6t + 1.7)
Substitute (6t+1.7) for T in N(T) and solve for N(6t + 1.7).
We have:
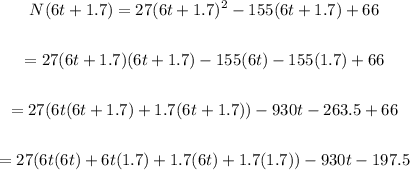
Solving further:

Therefore, the composite function is:
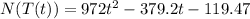
• (b). Find the time when the bacteria count reaches 26087.
Substitute 26087 for N(T(t)) and solve for t.
We have:
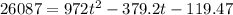
Equate to zero.
Subtract 26087 from both sides:
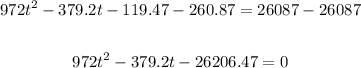
Solve using quadratic formula:
![t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/3cgw61gskglny4a505tle5b9wokluktv58.png)
Apply the standard quadratic formula to find the values of a, b, and c:
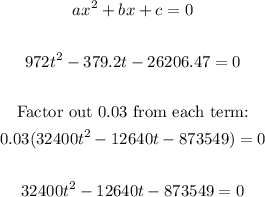
Thus, we have:
a = 32400
b = -12640
c = -873429
Input the values into the quadratic formula for solve for t:
![t=\frac{-(-12640)\pm\sqrt[]{113371720000_{}}}{2(32400)}](https://img.qammunity.org/2023/formulas/mathematics/college/p5tc9ufe56kjtmfoq79ftdk7pl5qy05acu.png)
Solving further:
![\begin{gathered} t=\frac{12640\pm200\sqrt[]{2834293}}{64800} \\ \\ t=\frac{316\pm5\sqrt[]{2834293}}{1620} \\ \\ t=\frac{316-5\sqrt[]{2834293}}{1620},\frac{316+5\sqrt[]{2834293}}{1620} \\ \\ t=-5.001,\text{ 5.}39 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zq84ivxou7mbhj149ofcd9onk1bivsko70.png)
We have the values:
t = -5.001
t = 5.39
Since the time cannot be negative, let's use the positive value.
Therefore, the time needed is 5.39 hours.
ANSWER:
5.39 hours.