Given
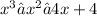
Step-by-step explanation
Part 1: Since the constant in the given equation is 4,the integer root must be a factor of 4. The possible values are
Answer:
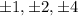
Part 2: The remainder theorem says when a polynomial a(x) is divided by a linear polynomial b(x) whose zero is x = k, the remainder is given by r = a(k). In this case for one of the possible values to be a root, it must give a zero result when inserted in the original expression.
Therefore,
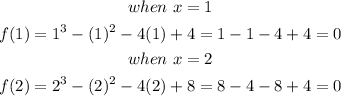
Answer: Therefore, 1 and 2 are roots of the polynomial
Part 3:
Let the last factor of the polynomial be ax+b
Therefore,
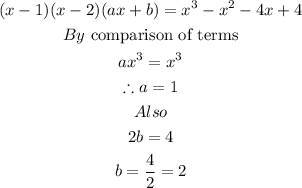
The factors of the equation are therefore;
Answer: (x-1)(x-2)(x+2)