Question

9. Rosie's Bakery just purchased an oven for $1,970. The owner expects the oven to last for 10years with a constant depreciation each year. It can then be sold as scrap for an estimatedsalvage value of $270 after 10 years. (20 points)a) Find a linear equation modeling the value of the oven, y, after x years of use.b) Find the value of the oven after 2.5 years.c) Find the y-intercept. Explain the meaning of the y-intercept in the context of this problem.d) Graph the equation of the line. Be sure to label the axes.

Answer 1

a)

The oven devaluated from $1970 to $270 in 10 years.

Since each year it looses the same value, divide the change in the price over the time interval to find the rate of change of the value with respect to time.

To find the change in price, substract the initial price from the final price:

`270-1970=-1700`

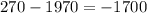
The change in price was -$1700.

Divide -1700 over 10 to find the change in the price per year:

`-(1700)/(10)=-170`

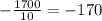
The initial value of the oven was $1970, and each year it looses a value of $170.

Then, after x years, the value will be equal to 1970-170x.

Then, the linear equation that models the value of the oven, y, after x years of use, is:

`y=-170x+1970`

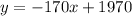
b)

To find the value of the oven after 2.5 years, substitute x=2.5:

`\begin{gathered} y_(2.5)=-170(2.5)+1970 \\ =-425+1970 \\ =1545 \end{gathered}`

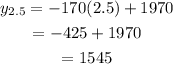
Then, the value of the oven after 2.5 years is $1545.

c)

To find the y-intercept, substitute x=0:

`\begin{gathered} y_0=-170(0)+1970 \\ =1970 \end{gathered}`

The y-intercept is the initial value of the oven when 0 years have passed.

d)