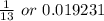Question

What is the probability that a card drawn randomly from a standard deck of 52 cards is a king? Express your answer as a fraction in lowest terms or a decimal rounded to the nearest millionth.

Answer 1

Case: Probability (52 cards)

A standard 52-card deck comprises 13 ranks in each of the four French suits: clubs (♣), diamonds (♦), hearts (♥) and spades (♠). Each suit includes three court cards (face cards), King, Queen and Jack, with reversible (double-headed) images. Each suit also includes ten numeral cards or pip cards, from one to ten. The card with one pip is known as an Ace. Each pip card displays the number of pips (symbols of the suit) corresponding to its number, as well as the appropriate numeral (except "A" for the Ace) in at least two corners.

Given: A standard deck of 52 cards

Required: Probability of selecting a king

Method:

Step 1: The probability formula:

`Pr(event\text{ A\rparen}=(n(A))/(Total)`

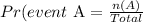
Step 2: The chances of obtaining event A (selecting King) is 4 out of 52.

`\begin{gathered} Pr(King)=(4)/(52) \\ Pr(King)=(1)/(13)OR\text{ 0.019231} \end{gathered}`

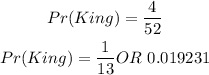
Final answer:

The probability of selecting a 'King' is:

`(1)/(13)\text{ }or\text{ 0.019231}`