Question

Given triangle DEF similar to triangle GHF. Enter segments in the blanks provided that would result in a true equation.

Answer 1

Given:

The triangles DEF is similar to GHF.

The objective is to find a similar ratio of DF/DE.

Step-by-step explanation:

Using the basic proportionality theorem, for the similar triangles DEF and GHF,

`(DE)/(GH)=(DF)/(GF)=(EF)/(HF)\text{ . . . . .. .(1)}`

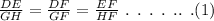
Considering the first two ratios of equation (1),

`(DE)/(GH)=(DF)/(GF)`

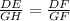
On interchanging the segments further,

`(DF)/(DE)=(GF)/(GH)`

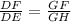
Hence, the required segment in the blanks is GF/GH.