We will focus on solving question 2a.
We are told that the parent function is
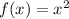
we want to identify the transformations applied to this function so we get the function

Note first we can start by multiplyin f(x) by -1. So get
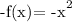
This multiplication by -1 represents a reflection across the x-axis. Now, if we add 4 to this equation, we get
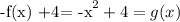
This move of adding 4 represent a shift of 4 units up.
So, to get the given function from the parent function, we should apply a reflection across the x-axis and the a shift of 4 units up