Question

Solve the equation.1/2K-(k+1/5)=1/10(k+2)

Answer 1

The equation is the following:

`(1)/(2)k-(k+(1)/(5))=(1)/(10)(k+2)`

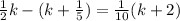
First let's eliminate the denominators. We can do that by multiplying both sides of the equation by 10:

`\begin{gathered} (10)/(2)k-10(k+(1)/(5))=k+2 \\ 5k-10k-2=k+2 \end{gathered}`

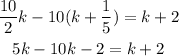
Then, we isolate the terms with the variable in one side of the equation, and the terms without the variable in the other side:

`\begin{gathered} 5k-10k-k=2+2 \\ -6k=4 \end{gathered}`

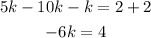
Finally, we divide both sides by the number multiplying the variable:

`\begin{gathered} (-6k)/(-6)=(4)/(-6) \\ k-(-4)/(6)=-(2)/(3) \end{gathered}`

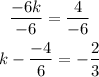
So the value of k is -2/3