Question

Find the shortest distance from A to B in the diagram below.A. 17 mB. 329−−√ mC. 505−−−√ mD. 10 m

Answer 1

Let us sketch out the part of the image needed,

To solve for the shortest distance from A to B, we will apply the Pythagoras theorem which states,

`\text{Hypotenuse}^2=Opposite^2+Adjacent^2`

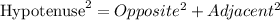
Given data

`\begin{gathered} \text{Hypotenuse}=a=\text{?} \\ \text{Opposite}=b=3=8m \\ \text{Adjacent}=c=6m \end{gathered}`

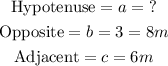
Solving for a,

`a^2=b^2+c^2`

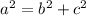
Substituting the values of b=8m and c=6m

`\begin{gathered} a^2=(8m)^2+(6m)^2 \\ a^2=64m^2+36m^2 \\ a^2=100m^2 \\ \end{gathered}`

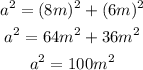
Take the square root of both sides

`\begin{gathered} \sqrt[]{a^2}=\sqrt[]{100m^2} \\ a=10m \end{gathered}`

Hence, the shortest distance from A to B is 10m.

The correct option is D.