Given:
For a 30-hour review course, the average score is 620.
For a 70-hour review course, the average score is 795.
To find: The linear equation and the average score for 54 hours review course.
Step-by-step explanation:
Let us take two points
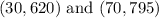
Using the two-point formula,
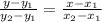
On substitution we get,

Thus, the linear equation is,
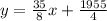
Therefore, for a 54-hour review course
The average score is,
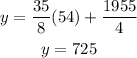
Thus, the average score for a 54-hour review course is 725.