1 Answer

Ryan Sparks · Answer 1 · 2023-02-17T08:25:42+0000

Step 1. The point we have is:

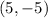
We will label this point as (x, y):

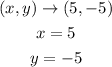
$\begin{gathered} (x,y)\to(5,-5) \\ x=5 \\ y=-5 \end{gathered}$

Step 2. We need to make a rotation of this point about the origin,

The rule for a rotation of 90° about the origin clockwise is:

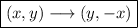
$\boxed{(x,y)\longrightarrow(y,-x)}$

Step 3. Applying the transformation from step 2 to the point from step 1:

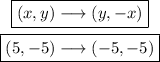
$\begin{gathered} \boxed{(x,y)\longrightarrow(y,-x)} \\ \boxed{(5,-5)\longrightarrow(-5,-5)} \end{gathered}$

We put the old y-value in the place of the new x-value, and we put the old x-value in the place of the new y-value with the opposite sign.

(-5,-5) is the result.

Answer:

(-5, -5)

Please log in or register to add a comment.