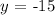1 Answer

Ilya Builuk · Answer 1 · 2023-04-01T01:41:55+0000

Solution:

The slope-intercept for a line with slope m and y-intercept b is given by the following equation:

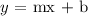
$y\text{ = mx + b}$

now, to find the slope m of a line that passes through the points (-8 -15) and (14 -15), we can use the following equation:

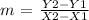
$m\text{ = }(Y2-Y1)/(X2-X1)$

where (X1,Y1) and (X2,Y2) are given points on the line. In this case, we have the points:

(X1,Y1) = (-8,-15)

(X2.Y2) = (14,-15)

now, replacing these points into the slope-equation, we get:

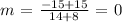
$m\text{ = }(-15+15)/(14+8)\text{ = 0}$

thus, the given line can be expressed as a constant function. That is, the provisional equation of the given line is:

$y\text{ = (0)x+b}$

this is equivalent to:

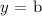
$y\text{ = b}$

to find b, we can replace any point on the line into the previous equation, for example, the point (x,y) = (14,-15) to obtain:

$y\text{ = }-15$

we can conclude that the line equation of the given line is:

$y\text{ = -15}$

Please log in or register to add a comment.