Question

9) Higher Order Thinking Make a conjecture about what happenswhen expressions are subtracted in the opposite order. What happenswhen the results are added? Support your conjecture with anexample in which several of the signs are negative.

Answer 1

Let the two expressions are 6a + 12b - 15c and -2a + 2b + 8c. First, subtract the second expression from the first:

`\begin{gathered} =6a+12b-15c-(-2a+2b+8c) \\ =6a+12b-15c+2a-2b-8c \\ =8a+10b-23c \end{gathered}`

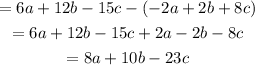
Now, subtract them in the reverse order, subtract the first from the second:

`\begin{gathered} =-2a+2b+8c-(6a+12b-15c) \\ =-2a+2b+8c-6a-12b+15c \\ =-8a-10b+23c \end{gathered}`

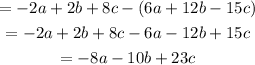
The second result is the negative of the first result.

Now, if the results are added then we get the answer zero.

`\begin{gathered} =8a+10b-23c+(-8a-10b+23c) \\ =8a+10b-23c-8a-10b+23c \\ =0 \end{gathered}`

Thus, we can say that when the expressions are subtracted in the opposite order, the results are negative of each other and when the results are added, we get zero as the answer.